Эренфест против специальной теории относительности

При осмыслении некоторых аспектов СТО возникла некоторая интеллектуальная «мина», а попытки ее обезвредить не привели к успеху. Решение найдено, см конец статьи. Получилось, что лоренцево сжатие для диска коменсируется механическим растяженим и диск Эренфеста с точки зрения неподвижного наблюдателя выглядит как самый обычный вращающийся диск радиуса R и длиной окружности 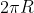. Пока  правлю статью, но не всю ( думаю, интересно посмотреть путь заблуждений и ошибок). Важные и правильные (с моей точки зрения) утвержения выделены синим цветом, а важные, но ошибочные выделены фиолетовым.

Получение формул СТО
Приведу стандартные рассуждения, восходящие к Альберту Эйнштейну (не факт что точно такие, но это некритично).
Сначала постулаты:
1. Инерциальные системы отсчета (ИСО) равноправны, все законы действуют одинаково и независимы от ориентации выбранной в ИСО системы координат.
2. Скорость света во всех ИСО системах одинакова (в любом направлении, согласно п1)

Для рассуждения будем ставить мысленный эксперимент с релятивистским поездом (как Эйнштейн).
Представим поезд, где в вагоне кондуктор-физик К ставит эксперименты (ИСО’), который движется вдоль платформы (оси Х) вправо со скоростью V относительно неподвижного наблюдателя Н (ИСО).

Пол вагона – точка отчета по вертикали для обоих наблюдателей.
Изготовим 3 экземпляра световых часов следующей конструкции: это стержень длиной метр, на одном конце которого излучатель и приемник, а на другом зеркало. Световой импульс излучается, доходит до зеркала, отражается и возвращается в приемник. Прибор считаем идеальным, от излучения до поглощения свет проходит точно 2 метра (до отражения 1 метр), все задержки нулевые. Т.к. скорость света во всех ИСО одинакова, у К и Н есть эталон метра и времени.

Время, за которое свет проходит 1 метр – это наша единица «секунда», и тогда скорость света=1м/сек. Два экземпляра часов отдадим К, а один оставим Н. Кондуктор движется мимо Н так, что событие, когда «хвост» (задняя стенка) вагона проезжает мимо неподвижного наблюдателя (начальные момент) считаем началом координат и для Н и для К (т.е. для этого события x=x’=t=t’=0). Итак, в начальный момент нулевые координаты для К и Н совпали (и по горизонтали и по вертикали и по времени – везде 0).
Пусть К и Н расположат свои часы вертикально так, чтобы нижний край с излучателем находился в начале координат в момент, когда хвост вагона проезжает мимо Н (это нулевое событие для обоих). Но совпадут ли зеркала? Предположим, для неподвижного наблюдателя поперечные размеры вагона сокращаются. Укрепим на зеркалах часов мелок. Н увидит, что мелок К чиркнет по часам Н, а мелок Н пройдет выше часов К. Но К увидит, что мелок его часов прошел выше, а мелок Н чиркнул по его часам! Значит, поперечные размеры не изменились и мелки чиркнули друг друга. К выводу о совпадении вертикальных размеров (или вообще говоря, перпендикулярных скорости размеров) можно прийти и другим путем: если размеры меняются, должно быть выделенное значение координаты, которое не изменяется, а это противоречит принципу равноправия всех ИСО).
Пусть в начальный момент часы К излучили световой импульс и через 2 секунды (по часам К) он попал в приемник.

Что видит Н? Он видит, что из движущихся часов в момент t0=0 вышел световой импульс (под углом!), в момент времени t импульс отразился от зеркала и в момент времени 2t попал в приемник. Для К импульс преодолел путь до зеркала за 1 секунду. Для Н пройденный путь 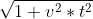(теорема Пифагора), значит поделив путь на скорость импульса (=1), получим время: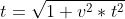, отсюда :. 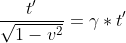Если кондуктор использует часы с длиной стержня t’ (время прохождения импульса 2t’), то Н увидит, что импульс прошел путь до зеркала за (использовали стандартное обозначение γ ("гамма") для выражения с корнем) Получилось, что для Н прошло больше времени, чем для К (эффект замедления времени в движущейся системе с точки зрения неподвижного наблюдателя).

К продолжает экспериментировать: он кладет вторые часы горизонтально, так чтобы для излучателя x’=0, а для зеркала x’=1. В начальный момент из обоих часов выходят импульсы, которые для К поглощаются через 2 секунды (для К нет разницы, вертикально или горизонтально расположены часы).
Что видит Н? Вертикальный импульс поглощается через γ*2 (расчет выше). Посчитаем горизонтальный. Пусть длина горизонтальных часов для Н равна L (точно не знаем, вдруг она другая). Тогда импульс доходит до зеркала за время 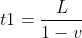 (зеркало "убегает" от импульса) и возвращается к приемнику за время  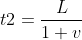(приемник "набегает" на импульс), итого от излучения до поглощения прошло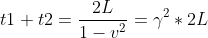 
Но это время должно совпадать с моментом, когда для Н вертикальные часы поглотят импульс (через время t= γ*2),отсюда L=1/γ, и получается, что продольные размеры сокращаются в γ раз. Н видит, что продольные часы (и ракета и К) сократились по оси "x" (но не по «y» и не по «z»- сокращаются размеры только в направлении движения).

Н понял, что интервалы и размеры, измеренные им, отличаются от тех, что измерил К. Н хочет найти формулу, связывающую координаты события x’,t’ в системе К и в своей системе. Для начала Н решил попробовать самые простые формулы – это линейное преобразование, т.е. x=ax’+bt’, t=ct’+dx’ Вспомним первый эксперимент с поперечными часами, когда событие получения сигнала x’=0, t’=2. Подставляем в формулы: t=c*2; x=b*2. Из расчетов выше Н известно, что t=γ*2,а x=v*t=v* γ*2 Отсюда c=γ,b= γ*v (два параметра найдены)
Теперь обратимся к рассмотренному выше событию, когда импульс отразится от зеркала в горизонтальных часах. Для К это событие имеет координаты x’=1, t’=1. Подставим их в формулы: x=a+γ*v, t= γ+d для получения значений Н. Выше показано, что длина для Н равна L=1/γ и поэтому импульс дойдет до зеркала через секунд (и это также координата зеркала в момент отражения, поскольку c=1).
Отсюда d=γ*v,a=γ и формулы приобретают вид: x=γ(x'+vt' );  t=γ(t'+vx').
Это формулы преобразования Лоренца (хотя их вывел Пуанкаре) пересчета координат событий из движущейся системы к неподвижной. Формулы пересчета из неподвижной получаются заменой знака у скорости: x'=γ(x-vt);  t'=γ(t-vx)
При с не равном 1 формулы такие:
Запомнить можно так: перед скобками «гамма», потом «своя» координата плюс-минус v*”чужая”. Знак перед vx такой же, как перед vt, а знак перед vt такой, чтобы точка X=0 в другой системе двигалась правильно.
Вот так, используя постулаты, теорему Пифагора и предположение о линейном преобразовании пространственно-временных координат путем несложных рассуждений пришли к формулам преобразования Лоренца/Пуанкаре.

Итак, формулы получены, пора их осмыслить и понять их следствия. И наблюдатель и кондуктор видят друг друга, видят все проводимые опыты и полученные результаты. Наблюдатель видит, какие временные интервалы и какие размеры получил К (и наоборот). Первое следствие - это то, что наблюдатель Н считает, что в поезде время течет медленней, чем у него. Второе - это сокращение длины поезда (для Н) и перрона (для К). Третье, не столь очевидное, но очень важное - то, что события, одновременные для К не одновременны для Н (и наоборот), если их координаты по оси движения различаются. Лучше всего понять, что видит каждый и почему - посмотреть x-t диаграмму Минковского, где показаны события и есть координатные сетки для Н и К. Именно относительность одновременности является ключом к ответу на вопрос - как может быть, что для Н вагон сократился, а для К - сократился перрон? Чтобы найти ответ на этот вопрос, надо сначала найти ответ на вроде бы элементарный вопрос: "как измерить длину предмета?" Очень просто - прикладываем предмет к линейке и делаем риски - начало предмета, конец предмета. А потом смотрим, сколько делений между рисками. Но как сделать риски, если предмет движется (слева направо, например)? Пусть сначала сделали левую риску, потом правую и получилась длина больше реальной (в процессе измерения предмет сдвинулся вправо!). Если сначала поставили правую риску, а потом левую, то намерили меньше по той же причине. Значит, просто надо ставить риски одновременно! Но то что одновременно для К, не одновременно для Н и наоборот, отсюда различия в измерениях для вагона и перрона. Формула t=γ(t'+vx'), переводящая время события для К (t') во время события для Н показывает, что из двух одновременных событий для К (одинаковые t') Н посчитает более поздним то, у которого больше x'. Если эти два события - измерение длины вагона (K одновременно ставит риски в начале и конце вагона), то Н увидит, что К сначала поставил риску в конце вагона, а потом в начале (и поэтому у него длина получилась больше).

Но хотя К и Н получают разные значения длины вагона и перрона, каждый считает свою длину правильной. Именно  эту, свою длину будут получать экспериментаторы во всех своих экпериментах. Положим, у Н есть друг-фотограф Ф, который стоит далеко по оси y и x=L/2 (L -длина вагона для Н). Этот фотограф включает сильную вспышку, свет от которой достигает координаты x=0 в момент t=0 (это было наше начало отсчета), отражается от вагона и возвращается в фотоаппарат. Если с другой стороны на платформе разместить фотоприемник, то он зафиксирует тень от вагона длиной L, т.е. длину вагона для Н.

Парадокс Эренфеста (релятивистский диск)
Данный парадокс был выдвинут Паулем Эренфестом в 1909 году после разработки Эйнштейном специальной теории относительности. Это тоже мысленный эксперимент. Любят физики-теоретики мысленные эксперименты: и средств не требуют и от технических проблем избавлены и анализируемые аспекты как на ладони. В этом эксперименты раскручиваем диск так, чтобы точки на краю двигались с субсветовой скоростью. Кусочек диска возле края движется почти как кусочек вагона выше, значит край диска должен испытывать лоренцево сокращение. А диаметр – нет (он поперек скорости). Возникает парадокс – диаметр то же, а окружность меньше. Решить его пытаются по-разному: то край стягивается и диск становится похож на сферу со срезанной верхушкой, то говорят, что диск деформируется из-за внутренних напряжений, то просто пишут, что диск разорвет и поэтому нет предмета обсуждения.  Или используют необычные метрики и диск снаружи вроде как диск, но внутри такой сложный. В общем, ни одно из объяснений не дало ощущения понимания и я придумал третий мысленный эксперимент, чтобы  перед построением физической картины просходящего "там, на диске, изнутри", понять что происходит здесь, на краю диска, как он должен выглядеть для неподвижных наблюдателей. Суть эксперимента - сделать так, чтобы локально для неподвижных наблюдателей все выглядело "почти как в инерциальной системе отсчета". Но потом оказывается, что  глобально  все выглядит совсем не так и возникает противоречие.

У меня получилось, что релятивистский диск с точки зрения неподвижного наблюдателя выглядит как самый обычный диск радиуса R и длиной окружности 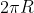 (см конец статьи).

 Поезд в кольцевом туннеле
Возьмем поезд из 2-3 или 10 вагонов и поместим его в большой кольцевой туннель радиуса R (а диаметр трубы только чтобы вагоны входили), разгоним до скорости V, близкой к скорости света. R у нас большое, поэтому поезд двигается почти как в первом эксперименте и должен сократиться в Y ("гамма") раз. Скорость у поезда огромная и Y большая (2 или даже 10). А ускорение – разве оно не будет влиять, как его учесть? Конечно, будет. Но его влияние должно зависеть от самого ускорения (меньше ускорение – меньше влияния). Как физик, я не могу представить, чтобы при нулевом ускорении происходило лоренцево сжатие, а при сколь угодно малом оно вдруг исчезало или в разы менялось его значение. Для тела, двигающегося по окружности, ускорение равно 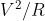 (это чистая геометрия). V около 1, а R мы можем увеличивать, пока влияние ускорения не станет малым (в мысленном эксперименте так можно поступать). Значит, длина поезда для неподвижного наблюдателя Н сократится практически в Y раз. А поскольку поезд едет в трубе по кольцу радиуса R, то и угловой размер поезда сократится в Y раз. А теперь ключевой момент эксперимента.  Поместим в туннель столько вагонов, чтобы они его полностью заполнили. Можно считать, что они на короткой сцепке, можно считать, что на длинной или даже на резинке. Главное – все вагоны одинаковы, все расстояния между ними одинаковы и они заполнили весь туннель. У каждого вагона свой двигатель и свой автопилот, так что это уже не поезд с головой и хвостом, а замкнутая цепь из вагонов. "Мы" (we) – неподвижные наблюдатели в центре и по периметру туннеля с синхронизованным общим временем. В нулевой момент времени из центра кольца всем вагонам идет сигнал "старт". Этот сигнал одновременно поступает на все вагоны и они синхронно (для нас) разгоняются. По достижению скорости V автопилоты прекращают разгон и вагоны едут с постоянной скоростью. Поскольку и вагоны и расстояния между ними должны претерпеть лоренцево сжатие, получается, что короткий поезд должен ехать в длинном туннеле. Но поезд изначально равномерно занимал туннель и приходим к противоречию (где и когда появится «разрыв»?).  Давайте в центр кольца поместим мощную вспышку, которая сделает моментальный снимок всех вагонов поезда (обклеим туннель фотобумагой - чего стесняться в мысленном эксперименте). Какие тени от вагонов должны получиться (пусть туннель прозрачный для лучей вспышки) - сжатые или нормальные?   Если смотреть с перрона на "эйнштейновский поезд", то сжимаются и вагоны и расстояния между вагонами (пространству все равно, чем оно заполнено) безо всяких напряжений. Пусть сначала разогнали поезд из 2 вагонов, а потом из N вагонов, заполняющих все кольцо. Получается, что локально лоренцево сжатие должно быть (согласно СТО), а глобально его быть не может. Представьте, что мимо  вагона, по касательной к окружности, движется космонавт с такой же скоростью (а ракета у него "изначально" такой же длины, как стоящий вагон). Этот момент видит неподвижный наблюдатель, находившийся по счастливой случайности рядом с точкой касания. Какой длины он будет видеть вагон, ракету? Я не могу разрешить эти противоречия (вагоны сожмутся - не сожмутся) иначе, как выводом, что поезд в туннеле не должен сокращаться. А отсюда следует, что и первый, «эйнштейновский» поезд тоже не должен сокращаться. Это и есть та интеллектуальная «мина», которая побудила меня создать эту запись.

Чтобы прояснить ситуацию (или еще больше запутать ) предложу соединить прямой и круговой поезда в одном эксперименте. Итак, где-то далеко-далеко стоят три вагона 1-2-3 прямого поезда на коротких сцепках. Одновременно (для нас, неподвижных наблюдателей) у них включаются двигатели, автопилоты по достижению скорости V их отключают (считаем, что силы трения нет). В момент времени t=0 вагоны едут мимо нас со скоростью V (это поезд1). По параллельной колее едут такие же вагоны 1-3, как в поезде1, только вместо сцепок и 2-го вагона вагоны 1-3 соединены резинкой (это поезд2). Резинка настолько растягиваемая, что никогда не рвется и настолько мягкая, что не влияет на движение вагонов. Поезд2 получили так: скопировали стоящий поезд1, а потом  сцепки и 2-й вагон убрали и соединили вагоны 1-3 резинкой (т.е расстояние между 1-м и 3-м вагонами точно такое же, как в поезде1). Они тоже в момент t=0 проезжают мимо нас. Будет смеяться, но эти обе ветки проходят рядом с кольцом, по которому со той же скоростью V несется поезд3 (точно такой же, как поезд2). При t=0 все три поезда встречаются (точнее, встречаются "задние стенки вагонов 1"). Какие длины вагонов всех трех поездов видит неподвижный наблюдатель в момент t=0? Может, появятся силы, которые "растянут" поезд3? 

Решение проблемы

Запутать, думаю, удалось. Теперь давайте распутываться. Ключ к решению проблемы во втором поезде, когда 2-й вагон и сцепки заменили резинкой. Пусть для стоящего поезда длина 1-го и 3-го вагона K, а длина резинки M. Тогда после разгона неподвижный наблюдатель увидит, что длина вагонов сократилась в  γ раз, а резинка не только не сократилась, но даже растянулась так, что расстояние между задними стенками вагонов такое же, как для стоящего поезда, т.е. K+M. Это называется парадокс Белла. В случае поезда с жесткими сцепками они не дадут вагонам разойтись и общая длина поезда сократится. Поэтому картинка волнующей встречи трех поездов должна выглядеть примерно так: 

Для вагонов в туннеле происходит тоже самое - сжатие самих вагонов компенсируется растяжением резинки. Вагоны в круговом туннеле сокращаются, а поезд в целом - нет. Но как быть с диском Эренфеста, у него нет резинок? Мысленно разрежем диск на тонкие кольца. Возьмем кольцо радиуса R, скорость точек на нем 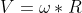. Разрежем кольцо, получим полоску длиной 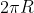, растянем эту полоску в  γ раз, раскрутим до скорости V и склеим в кольцо. В результате с точки зрения неподвижного наблюдателя получится кольцо радиуса R и длиной окружности  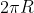 , и внутренней длиной окружности 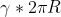. Диск Эренфеста как бы собран из таких "растянутых" полосок, собранных в "нормальный" плоский диск. Можно ничего не резать и не склевать, а просто считать, что вращающееся кольцо имеет радиус R, внешнюю длину  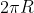и внутреннюю длину  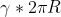 , причем материал кольца внутри растянут в  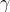раз. Неподвижный наблюдатель видит абсолютно обычный диск (радиуса R, длиной  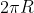 ), только быстровращающийся. Выходит, для диска Эренфеста лоренцево сжатие круговых слоев диска компенсируются их механическим растяжением. Если на диск по периметру нанести полоски с расстоянием L между ними и раскрутить его, то расстояние между полосками с точки зрения неподвижного наблюдателя почти не изменится, точнее немного возрастет из-за увеличения радиуса самого диска  (абсолютно твердых материалов не бывает). Может, эспериментаторы смогут сделать такой эксперимент (с полосками)? 

Если материал диска не позволит растянуть внешний слой в 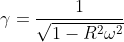 раз, где  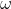-угловая скорость, а R-радиус диска, то диск просто разрушится (поэтому материал надо брать эластичный).  Интересно посчитать, какие там должны возникать напряжения. Что же произойдет с поездом, у которого вагоны соединены не резинками, а жесткими сцепками? Общая длина вагоны+сцепки для неподвижного наблюдателя должна сохраниться, а это означает, что вагоны и сцепки растянутся (или лопнут).