Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве
Я обнаружила, что существуют три основных случая взаимного расположения прямых в пространстве и связанные с этим закономерности.
- Случай, когда прямые параллельны друг другу. Расстояние между ними одинаково везде. А значит, для нахождения этого расстояния достаточно совершить всего один шаг – опустить перпендикуляр из любой точки одной прямой к другой прямой. Причем, неважно от какой прямой опускать перпендикуляр.
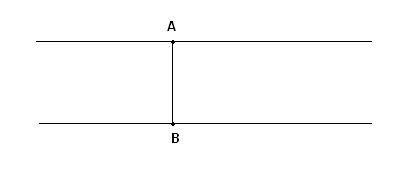
(рис.1)
Мы можем представить эти прямые лежащими в разных плоскостях, но всегда можно провести или представить плоскость, в которой они обе лежат.
2. Случай, когда прямые лежат в перпендикулярных плоскостях, и одна прямая параллельна линии пересечения плоскостей, а вторая пересекает её под неким углом.
Самый простой вариант – когда этот угол равен 90 градусов.
Тогда для нахождения минимального расстояния между прямыми надо проделать всего два шага:
1 – из любой точки одной прямой (А) опустить перпендикуляр ко второй прямой,
2 – из полученной точки В опустить перпендикуляр к первой прямой. Отрезок СВ – это и есть минимальное расстояние между прямыми.
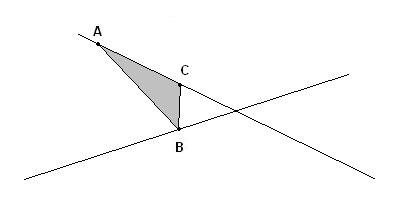
(рис.2)
Треугольник АВС – прямоугольный треугольник, степень вытянутости которого зависит от выбранной изначально точки.
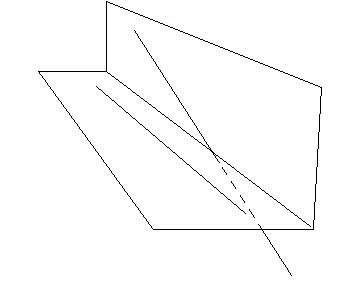
(рис.3)
Но если угол не равен 90 градусам, то мы получим не один прямоугольный треугольник, а множество:
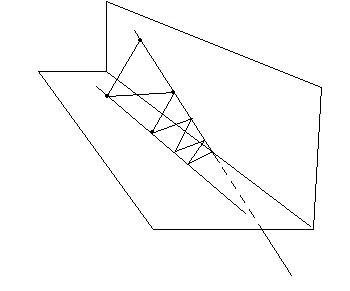
(рис.4)
Отрезки, соединяющие прямые на рисунке 4 – это перпендикуляры, опущенные от одной прямой к другой. Если эти отрезки уменьшаются, то мы приближаемся к искомому месту, если отрезки увеличиваются, то мы удаляемся от него.
Подобное поведение указывает, что наши прямые лежат в перпендикулярных плоскостях, причем, одна из них пересекает линию пересечения плоскостей под непрямым углом.
3. И наконец, третий, самый интересный случай – когда прямые лежат в разных плоскостях, которые не перпендикулярны и не параллельны друг другу.
Рассмотрим этот случай поподробнее.
Пусть у нас есть такие прямые aи b.
Через одну из этих прямых мы можем провести взаимно перпендикулярные плоскости. Тогда вторая прямая пересечёт эти плоскости в неких точках А и В (см. рисунок).
Из этих точек мы можем опустить перпендикуляры к прямой a. В результате у нас получатся два отрезка – AXи BY, лежащие в этих перпендикулярных плоскостях.
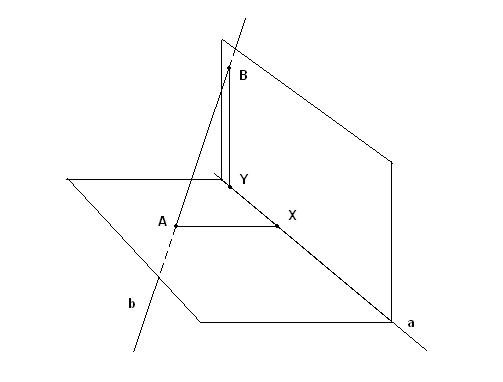
(рис.5)
Если мы соединим попарно полученные точки, то получим трехмерную фигуру, четырехгранник, у которого все грани являются прямоугольными треугольниками:
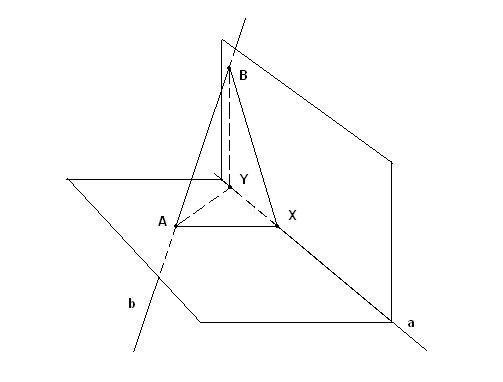
(рис.6)
Чтобы вырезать и собрать такую трехмерную фигуру из бумаги, понадобится вот такая развертка:
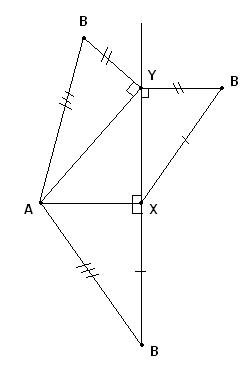
(рис.7)
Самое интересное, что именно в этом, третьем случае нахождение минимального расстояния между прямыми aи bтребует ровно три шага:
1) Из точки А на одной прямой опустить перпендикуляр ко второй прямой, получаем точку В.
2) Из точки В опускаем перпендикуляр ко второй прямой, получаем точку С.
3) Из точки С опускаем перпендикуляр к первой прямой, получаем СD. CD– это и есть минимальное расстояние между двумя прямыми.
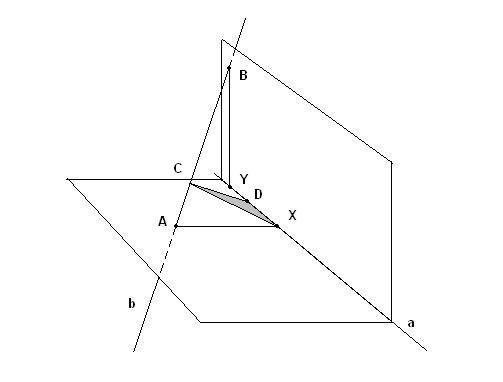
(рис.8)














Комментарии
Любопытно было бы посмотреть, а я предупреждал - геометрией иногда можно сказать больше чем словами.